Евклид — биография, новости, личная жизнь

Описание и доказательство алгоритма

Для целых чисел алгоритм состоит из соотношений, количество которых равно числу элементов. Если предположить, что а и b являются целыми и неравными нулю значениями, то для них выполняется соотношение a > b > R1 > … > Rn. Величинами R с определенными индексами являются остатки от деления а на некоторое значение Q1 и b на Q2. Описывается процесс такими формулами:

1. а = b * q0 + R1.
2. b = R1 * q1 + R2.
3. R1 = R2 * Q2 + R3.
4. Rn-1 = Rn * Qn.

На последнем этапе не должно быть остатка. Для отрезков применяется геометрический алгоритм. Чтобы найти наибольший общий отрезок, нужно из большего вычесть меньший, а затем заменить первый их разностью. Операцию следует завершить при равенстве двух отрезков. Реализуется данный алгоритм при помощи циркуля и линейки. Для доказательства алгоритма Евклида следует взять пару чисел f и g, для которых можно привести такие утверждения:

1. Делители f и g — общие делители (f — g) и g.
2. Делители (f — g) и g — общие делители f и g.
3. Когда f > g, тогда НОД (f, g) = НОД (f — g, g).
4. НОД (f, 0) = f.

Для доказательства следует ввести новую переменную z. Она является общим делителем для f и g. Кроме того, разность f — g также делится на z. Из предположения f = z * k и g = z * s следует, что f — g = z * k — z * s = z * (k — s). Иными словами, z — общий множитель для f — g. Из соотношения можно доказать, что z делит не только разность, но и сумму: f — g + g = f. Следовательно, z — общий делитель для f и g.

Следует отметить, что методика для нескольких чисел (трех и более) аналогичная. В этом случае нужно брать не одну разность, а две, в которой будет присутствовать минимальное число. Данный алгоритм применяется в построении программного обеспечения. Однако перед написанием кода следует сначала составить блок-схему. Она позволит избежать ошибок, а также внимательно сосредоточиться на проекте.

Интересные факты из жизни

Несколько любопытных фактов из биографии Евклида:

1. Самый древний известный математический трактат принадлежит Евклиду.
2. До сих пор нет данных о месте рождения и смерти великого ученого. Однако известно место занятий Евклида примерно 2400 лет назад и место его нахождения — Александрия. Интересно, что этот городок сегодня — второй по размерам в Египте после Каира;
3. Евклид смог создать 4 книжки по коническому виду сечений.
4. Фундаментальный труд «Начала» считается настолько важным для науки, что до сих пор его используют в жизни. Интересно, что есть другие публикации с подобным наименованием, но самый популярный — труд Евклида».
5. С самой юности Евклид обучался у именитого ученого Платона, обучавшего Аристотеля в Древней Греции. Сам же Платон обучался у Сократа.
6. По традиции геометрия сегодня носит название этого ученого.
7. Есть легенда, что когда один раз ученик величайшего математика спросил у него, как геометрия может помочь ему в жизни, то Евклид дал ему денег и прогнал с занятий.
8. Евклид до сих пор считается автором многочисленных книг, чье авторство не было подтверждено. Это разные труды, к примеру, публикации по музыке, философии и медицине. Официально известно, что великий ученый сделал открытие в оптических и астрономических областях.
9. Сегодня признают римановскую, лобачевскую и евклидову геометрию. Последняя — самая традиционная и часто используемая.
10. В первый раз евклидовский труд перевели в конце восемнадцатого века. При этом «Начала» впервые были переведены на армянский язык в одиннадцатом веке.
11. Любимая фраза: «Нет царского пути в геометрии».

В целом, Евклид является отцом геометрии, и он не случайно так называется. Он первым сделал сложное понятным и дал толчок развитию естественных наук. Его книги неоценимы по значимости и применяются сегодня в области математических и геометрических наук во всем мире.

Неевклидова геометрия

И только через 2 с лишним тысячи лет российский математик Лобачевский усомнился в безраздельной справедливости геометрии Евклида. Он вывел «свою собственную» геометрию, которая базировалась не на плоскости, а на псевдосфере. Интересно, что все Аксиомы, выведенные Евклидом, сохранялись. Кроме одной – о параллельных прямых.

Кроме Лобачевского, «свою» геометрию вывел и немецкий математик Риман. В настоящее время три геометрии странным образом сосуществуют в мире – Евклидова, Римана и Лобачевского.

Так ли это было, как описывают некоторые истории о Евклиде, а, может, и вовсе ничего подобного не было – не столь уж важно. Автор «Математических начал» навечно вписал свое имя в анналы науки, там он и останется – наряду с такими гениями, как Ньютон, Галилей, Сократ или Пифагор

«Начала» Евклида

Ватиканский манускрипт, т.1, 38v — 39r. Euclid I prop. 47 (теорема Пифагора)

Основное сочинение Евклида называется Начала. Книги с таким же названием, в которых последовательно излагались все основные факты геометрии и теоретической арифметики, составлялись ранее Гиппократом Хиосским, Леонтом и Февдием. Однако Начала Евклида вытеснили все эти сочинения из обихода и в течение более чем двух тысячелетий оставались базовым учебником геометрии. Создавая свой учебник, Евклид включил в него многое из того, что было создано его предшественниками, обработав этот материал и сведя его воедино.

Начала состоят из тринадцати книг. Первая и некоторые другие книги предваряются списком определений. Первой книге предпослан также список постулатов и аксиом. Как правило, постулаты задают базовые построения (напр., «требуется, чтобы через любые две точки можно было провести прямую»), а аксиомы — общие правила вывода при оперировании с величинами (напр., «если две величины равны третьей, они равны между собой»).

Евклид открывает врата Сада Математики. Иллюстрация из трактата Никколо Тартальи «Новая наука»

В I книге изучаются свойства треугольников и параллелограммов; эту книгу венчает знаменитая теорема Пифагора для прямоугольных треугольников. Книга II, восходящая к пифагорейцам, посвящена так называемой «геометрической алгебре». В III и IV книгах излагается геометрия окружностей, а также вписанных и описанных многоугольников; при работе над этими книгами Евклид мог воспользоваться сочинениями Гиппократа Хиосского. В V книге вводится общая теория пропорций, построенная Евдоксом Книдским, а в VI книге она прилагается к теории подобных фигур. VII—IX книги посвящены теории чисел и восходят к пифагорейцам; автором VIII книги, возможно, был Архит Тарентский. В этих книгах рассматриваются теоремы о пропорциях и геометрических прогрессиях, вводится метод для нахождения наибольшего общего делителя двух чисел (известный ныне как алгоритм Евклида), строятся чётные совершенные числа, доказывается бесконечность множества простых чисел. В X книге, представляющей собой самую объёмную и сложную часть Начал, строится классификация иррациональностей; возможно, что её автором является Теэтет Афинский. XI книга содержит основы стереометрии. В XII книге с помощью метода исчерпывания доказываются теоремы об отношениях площадей кругов, а также объёмов пирамид и конусов; автором этой книги по общему признанию является Евдокс Книдский. Наконец, XIII книга посвящена построению пяти правильных многогранников; считается, что часть построений была разработана Теэтетом Афинским.

В дошедших до нас рукописях к этим тринадцати книгам прибавлены ещё две. XIV книга принадлежит александрийцу Гипсиклу (ок. 200 г. до н. э.), а XV книга создана во время жизни Исидора Милетского, строителя храма св. Софии в Константинополе (начало VI в. н. э.).

Начала предоставляют общую основу для последующих геометрических трактатов Архимеда, Аполлония и других античных авторов; доказанные в них предложения считаются общеизвестными. Комментарии к Началам в античности составляли Герон, Порфирий, Папп, Прокл, Симпликий. Сохранился комментарий Прокла к I книге, а также комментарий Паппа к X книге (в арабском переводе). От античных авторов комментаторская традиция переходит к арабам, а потом и в Средневековую Европу.

В создании и развитии науки Нового времени Начала также сыграли важную идейную роль. Они оставались образцом математического трактата, строго и систематически излагающего основные положения той или иной математической науки.

Аксиомы

Евклид говорил, что аксиомы – это утверждения, не требующие доказательств, но при этом он понимал, что слепое принятие на веру этих утверждений не может использоваться в построении математических теорий и формул. Он осознавал, что даже аксиомы должны быть подкреплены неоспоримыми доказательствами. А потому учёный начал приводить логические заключения, подтверждавшие его геометрические аксиомы и теоремы. Для лучшего понимания этих аксиом, он разделил их на две группы, которые назвал «постулатами». Первая группа известна как «общие понятия», состоящие из признанных научных утверждений. Вторая группа постулатов является синонимом самой геометрии. Первая группа включает такие понятия, как «целое больше суммы частей» и «если две величины порознь равны одной и той же третьей, то они равны между собой». Вот лишь два из пяти постулатов, записанных Евклидом. Пять постулатов второй группы относятся непосредственно к геометрии, утверждая, что «все прямые углы равны между собой», и что «от всякой точки до всякой точки можно провести прямую».

Научная деятельность математика Евклида процветала, и в начале 1570-х г.г. его «Начала» были переведены с греческого языка на арабский, а затем и на английский язык Джоном Ди. С момента своего написания, «Начала» были перепечатаны 1 000 раз и, в конце концов, заняли почётное место в учебных классах XX столетия. Известно множество случаев, когда математики пытались оспорить и опровергнуть геометрические и математические теории Евклида, но все попытки неизменно оканчивались провалом. Итальянский математик Джироламо Саккери стремился усовершенствовать труды Евклида, но оставил свои попытки, не в силах отыскать в них ни малейшего изъяна. И лишь спустя столетие новая группа математиков сможет представить новаторские теории в области геометрии.

биография

Точная дата рождения Евклида неизвестна. Исторические записи позволили определить его местонахождение где-то в 325 году до нашей эры..

По его образованию, по оценкам, имело место в Афинах, потому что работа Евклида показала, что он глубоко знал геометрию, которая была создана из школы Платона, разработанной в этом греческом городе.

Этот аргумент поддерживается до тех пор, пока не будет выведено, что Евклид, казалось, не знал работы афинского философа Аристотеля; по этой причине нельзя утверждать окончательно, что образование Евклида было в Афинах.

Преподавательская работа

В любом случае известно, что Евклид учил в Александрии, когда командовал королем Птолемеем I Сотером, который основал династию Птолемеев. Считается, что Евклид проживал в Александрии около 300 г. до н.э., и там он создал школу, посвященную преподаванию математики..

В этот период Евклид приобрел большую известность и признание благодаря своим способностям и навыкам учителя..

Анекдот, связанный с королем Птолемеем I, выглядит следующим образом: некоторые записи указывают, что этот король попросил Евклида научить его быстрому и краткому способу понимания математики, чтобы понимать и применять их.

Учитывая это, Евклид указал, что нет никаких реальных способов получить это знание. Намерение Евклида с этим двойным смыслом состояло также в том, чтобы показать царю, что, будучи не могущественным и привилегированным, может понимать математику и геометрию.

Личные характеристики

Вообще, Евклид изображался в истории как спокойный, очень добрый и скромный человек. Также сказано, что Евклид полностью понимал огромную ценность математики, и что он был убежден, что знание само по себе бесценно.

На самом деле, есть еще один анекдот об этом, который превзошел наше время благодаря доктору Хуану де Эстобео.

По-видимому, на уроке Евклида, в котором рассматривался предмет геометрии, студент спросил его, какую пользу он получит, получив эти знания. Евклид твердо ответил ему, объяснив, что знание само по себе является самым бесценным элементом, который существует.

Поскольку ученик, очевидно, не понимал и не подписывался на слова своего учителя, Евклид дал указание своему рабу дать ему несколько золотых монет, подчеркнув, что выгода от геометрии была гораздо более превосходной и глубокой, чем денежное вознаграждение..

Кроме того, математик указал, что нет необходимости получать прибыль от каждого знания, приобретенного в жизни; Сам факт получения знаний сам по себе является величайшим достижением. Это было видение Евклида в отношении математики и, в частности, геометрии.

смерть

Согласно записям в истории, Евклид умер в 265 году до нашей эры в Александрии, городе, в котором он прожил большую часть своей жизни..

Псевдо-Евклид

Евклиду приписываются два важных трактата об античной теории музыки: «Гармоническое введение» («Гармоника») и «Деление канона» (лат. Sectio canonis). Традиция приписывать «Деление канона» Евклиду идёт ещё от Порфирия. В старинных рукописях «Гармоники» авторство приписывается Евклиду, некоему Клеониду, а также александрийскому математику Паппу. Генрих Мейбомrude (1555—1625) снабдил «Гармоническое введение» обстоятельными примечаниями, и вместе с «Делением канона» приписал их к трудам Евклида.

При последующем подробном анализе этих трактатов было определено, что первый написан в аристоксеновской традиции (например, в нём все полутоны считаются равными), а второй по стилю — явно пифагорейский (например, отрицается возможность деления тона ровно пополам). Стиль изложения «Гармонического введения» отличается догматизмом и непрерывностью, стиль «Деления канона» несколько схож с «Началами» Евклида, поскольку содержит теоремы и доказательства.

После критической публикации «Гармоники» знаменитым немецким филологом Карлом Яном (1836—1899) этот трактат стали повсеместно приписывать Клеониду и датировать II в. н.э. В русском переводе (с комментариями) его впервые издал Г. А. Иванов (Москве, 1894). «Деление канона» ныне одна часть исследователей считает аутентичным сочинением Евклида, а другая — анонимным сочинением в традициях Евклида. Последние по времени русские переводы «Деления канона» опубликованы (в версии Порфирия) В.Г.Цыпиным и (в версии Боэция) С.Н.Лебедевым. Критическое издание оригинального текста «Деления канона» выполнил в 1991 г. А.Барбера.

• Назад

• Вперёд

Добавить комментарий

Научная деятельность и открытия

Вся жизнь ученого прошла в александрийских стенах, поэтому и его научная деятельность с открытиями состоялась здесь. Образование он получил от платоновских учеников, поэтому от них же и перенял взгляды, которые и помогли ему сформировать свой класс математики и стать преподавателем.

Предшественниками Евклида были знаменитые математики Фалес с Пифагором и Аристотелем, которые сделали фундаментальные открытия в области тригонометрической науки. Но это были разрозненные части и не представляли собой одну большую логически выстроенную цепочку.

Как и современники, математик и его ученики любили систематичные и логичные знания. Именно поэтому всю свою научную деятельность Евклид бросил на систематизацию ранее полученных знаний и их дополнение. В каждой из своих книг «Начал» он дает основные понятия, использованные учеными ранее, а затем вводит основные аксиомы и постулаты геометрии, которые упростили работу его потомкам.

Так, с первой по четвертую книгу даются понятия и постулаты из трудов Пифагора и его последователей, в пятой книге — учение о пропорциях, с шестой по девятую книгу — знание о числах, а в последних — публикации о площадях с плоскостями и пространствами (основы стереометрии), иррациональности, учении о правильных телах.

Интересно, что публикация автора дала возможность писать последующие научные работы в области математики и получать новые знания о ней.

Свои открытия ученый сделал в той же области. Он ввел понятие точки, прямой, плоскости и движения, разработал постулаты для создания определенных геометрических фигур в любой области, понятие о свете, зеркалах, преломлении световых лучей, ввел элементарную теорию музыки, создал труд касательно использования геометрии при изучении астрономии и ошибках, которые возникают при формировании геометрических доказательств.

Кроме того, математик сделал небольшие открытия в области механики и дал понятие удельному весу тел.

Различные вариации

Кольцо является алгебраическим выражением или структурой, в которой применяются операции сложения (обратимого) и умножения эквивалентные соответствующим действиям над некоторыми числами. Примером считается обобщенные множества целых, дробных и комплексных чисел. Более сложный пример — различные функции с элементами кольца. Если к данному множеству применима лема Евклида, то его называют Евклидовым кольцом. К ним относятся кольца целых чисел и многочленов.

Для многочлена вида Z от одной неизвестной g над некоторым полем (функцией) Z определена операция деления. Последняя выполняется только с остатком. Если применить к нему правило Евклида, то получится последовательность остатков в виде полиномов. Для примера следует разобрать такую задачу: пусть cont (w) является НОД для коэффициентов f (w) из полинома Z. При делении f (w) на cont (w) образуется примитивная часть многочлена primpart (f (w)). Необходимо найти НОД Р1 (g) и Р2 (g). Если числа являются целыми, то в этом случае верны такие тождества:

1. сont (НОД {Р1 (g), Р2 (g)}) = НОД{сont (Р1 (g)), сont (Р2 (g))}.
2. primpart (НОД {Р1 (g), Р2 (g)}) = НОД{primpart (Р1 (g)), primpart (Р2 (g))}.

Следовательно, поиск НОД для двух многочленов нужно свести к поиску НОД примитивных полиномов. Для примитивных полиномов Р1 (g) и Р2 (g), принадлежащих Z, выполняется такое соотношение между их степенями: deg (Р1 (g)) = m и deg (Р2 (g)) = n (m > n). Деление с остатком осуществляется по псевдоделимости, поскольку иногда выполнить первую процедуру невозможно.

В результате этого вводят специальный алгоритм для псевдоделения, результатом которого является псевдоостаток. Его обозначают «prem». Формула операции псевдоделения имеет такой вид с учетом псевдочастного Q (g) и псевдоостатка R (g): * P1 (g) = P2 (g) * Q (g) + R2 (g) при deg (R (g)) < deg (P2 (g)). Следовательно, P1 (g) и P2 (g) принадлежат Z при условии, что deg (P1) = n1 >= deg (P2) = n2. На основании полученных результатов лема Евклида состоит из таких пунктов:

1. Найти НОД: НОД{сont (Р1 (g)), сont (Р2 (g))}.
2. Расчет примитивных частей: ‘ = primpart (P1 (g)) и ‘ = primpart (P2 (g)).
3. Последовательность псевдоостатков полиномного типа: ‘, ‘, ‘ = prem (‘, ‘), ‘ = prem (‘, ‘),…, ‘ = prem (‘, ‘).
4. Возвратить результат: если deg (Pn (g)) = 0, то вернуть НОД{сont (Р1 (g)), сont (Р2 (g))}. Иначе — выражение в первом пункте нужно умножить на primpart (Pn (g)).

Евклид и античная философия[править | править код]

Йос ван Вассенхове (Юстус из Гента). Евклид, ок. . Урбино

Уже со времён пифагорейцев и Платона арифметика, музыка, геометрия и астрономия (т.наз. «математические» науки) рассматривались в качестве образца систематического мышления и предварительной ступени для изучения философии. Не случайно возникло предание, согласно которому над входом в платоновскую Академию была помещена надпись «Да не войдёт сюда не знающий геометрии».

Геометрические чертежи, на которых при проведении вспомогательных линий неявная истина становится очевидной, служат иллюстрацией для учения о припоминании, развитого Платоном в Меноне и других диалогах. Предложения геометрии потому и называются теоремами, что для постижения их истины требуется воспринимать чертёж не простым чувственным зрением, но «очами разума». Всякий же чертёж к теореме представляет собой идею: мы видим перед собой эту фигуру, а ведём рассуждения и делаем заключения сразу для всех фигур одного с ней вида.

Некоторый «платонизм» Евклида связан также с тем, что в Тимее Платона рассматривается учение о четырёх элементах, которым соответствуют четыре правильных многогранника (тетраэдр — огонь, октаэдр — воздух, икосаэдр — вода, куб — земля), пятый же многогранник, додекаэдр, «достался в удел фигуре вселенной». В связи с этим Начала могут рассматриваться как развёрнутое со всеми необходимыми посылками и связками учение о построении пяти правильных многогранников — так называемых «платоновых тел», завершающееся доказательством того факта, что других правильных тел, кроме этих пяти, не существует.

Для аристотелевского учения о доказательстве, развитого во Второй аналитике, Начала также предоставляют богатый материал. Геометрия в Началах строится как выводная система знаний, в которой все предложения последовательно выводятся одно за другим по цепочке, опирающейся на небольшой набор начальных утверждений, принятых без доказаельства. Согласно Аристотелю, такие начальные утверждения должны иметься, так как цепочка вывода должны где-то начинаться, чтобы не быть бесконечной. Далее, Евклид старается доказывать утверждения общего характера, что тоже соответствует любимому примеру Аристотеля: «если всякому равнобедренному треугольнику присуще иметь углы, в сумме равные двум прямым, то это присуще ему не потому что он равнобедренный, а потому что он треугольник» (An. Post. 85b12).

дальнейшее чтение

• ДеЛейси, Эстель Аллен (1963). Евклид и геометрия. Нью-Йорк: Франклин Уоттс.
• Кнорр, Уилбур Ричард (1975). Эволюция евклидовых элементов: исследование теории несоизмеримых величин и ее значение для раннегреческой геометрии. Дордрехт, Голландия: Д. Рейдел. ISBN 978-90-277-0509-9.
• Мюллер, Ян (1981). Философия математики и дедуктивная структура в элементах Евклида. Кембридж, Массачусетс: MIT Press. ISBN 978-0-262-13163-6.
• Рид, Констанс (1963). Долгий путь от Евклида. Нью-Йорк: Кроуэлл.
• Сабо, Арпад (1978). Начало греческой математики. ЯВЛЯЮСЬ. Унгар, пер. Дордрехт, Голландия: Д. Рейдел. ISBN 978-90-277-0819-9.

[править] Научные труды

Евклид получил научное образование от учеников Платона и был приглашён в Александрию Птолемеем, сыном Лага; здесь, в Александрии он основал школу математики. Из его сочинений дошли только «Элементы геометрии», книга под заглавием «Данные», трактата по геометрической оптике и катоптрике и часть сочинения о делении площадей многоугольников.

Математики более позднего времени Папп Александрийский и Прокл упоминают на не дошедшие до нас книги Евклида: четыре книги о конических сечениях, две книги о местах на поверхности и на три книги «Поризмы».

Наиболее знаменита книга Евклида «Элементы». Он первый дал настолько стройное, систематическое и изящное изложение геометрии прямых линий и круга, что в Англии до 20 в. при начальном обучении геометрии придерживаются изложения Евклида. Изложение «Геометрии» Евклида состоит из 13 книг, к которым присоединяют 2 книги о 5 правильных многогранниках, хотя открытие их несправедливо приписывают Гипсиклу Александрийскому (жил 150 лет позднее Евклида). Собственно геометрия прямых линий, кругов и плоских фигур заключается в первых шести книгах, а в пяти последних книгах изучаются поверхности и тела, в 7-й, 8-й и 9-й книгах рассматриваются свойства чисел, в 10-й рассматриваются в подробности величины несоизмеримые. Под «данными» подразумеваются те величины, которые на основании теорем, доказанных в «Элементах», могут быть определены из условий задачи. Если, например, задана на плоскости определенная точка и круг определенного радиуса, центр которого имеет вполне определенное положение, то длины и направления касательных из точки к кругу суть прямые «данные». Что такое «поризмы» — точно неизвестно. Папп и Прокл, говоря о поризмах, выражаются столь неясно, что нельзя составить себе представления об этом предмете. Папп, между прочим, говорит о поризмах как о каком-то особом методе, применяемом с успехом при решении многих трудных задач. Возможно, поризмы представляют упрощенный способ вывода некоторых лемм либо представляют собой нечто подобное сокращенному методу аналитической геометрии или, может быть, нечто подобное тем методам, которые употребительны в высшей геометрии. В «Началах» Евклид описывает метрические свойства пространства, которое современная наука называет Евклидовым пространством. Евклидово пространство является ареной физических явлений классической физики, основы которой были заложены Галилеем и Ньютоном. Это пространство пустое, безграничное, изотропное, имеющее три измерения.

Прокл (410—485 гг. н. э.) рассказывает, что Птолемей I спросил Евклида, нет ли короткого пути для понимания геометрии, чем тот, который изложен в «Началах», на что Евклид ответил: «В геометрии нет царского пути».

Евклид придал математическую определенность атомистической идее пустого пространства, в котором движутся атомы.

Написал также работы по астрономии, оптике, теории музыки.

Фильмы

В кино Эвклид Кюрдзидис попал именно благодаря своей экзотической для России внешности. На втором курсе ВГИКа его заметил режиссер Владимир Мотыль, который на тот момент снимал картину «Несут меня кони». В ленте парню досталась эпизодическая роль грека, ради чего он подстриг волосы и отрастил усы.

В дальнейшем Эвклида стали приглашать на характерные роли различных иностранцев. В фильме 1997 года «Интермед» он сыграл французского машиниста, а в «Свидании вслепую» 2000 года — итальянца.

Эвклид Кюрдзидис в фильме «Бабий Яр»

С 2001 года Эвклида активно снимают в образах чеченцев и людей восточной нации. Впервые в подобном амплуа он появился в телесериале «Мужская работа», где сыграл чеченского боевика по прозвищу «Шрам». В 2002 году он принял участие в съемках фильма «Война», где сыграл одну из своих любимых ролей в карьере — пожилого чабана Руслана Шамаева. Чтобы не стать актером одного амплуа, Эвклид стал более избирательно относиться к выбору подобных ролей.

В 2003 году Кюрдзидис принял участие в съемках фильма «Бабий Яр», повествующем о страшных событиях во время Второй Мировой войны. Продюсером фильма выступил немец Артур Браунер, а режиссером стал американец Джеф Кэнью. Хотя актеру досталась небольшая роль, съемки серьезно повлияли на его восприятие мира и отношение к войне.

Эвклид Кюрдзидис в фильме «Зверобой-3»

В 2005 году на экраны вышел сериал «Мой личный враг» режиссера Владимира Попкова, где актер сыграл нетипичную для себя роль богатого француза, который приехал в Россию писать книгу. Для этой роли Эвклиду пришлось учить французский язык, совмещая его с изучением английского — в то же время он принимал участие в пробах голливудского фильма. Картина принесла Кюрдзидису заслуженный успех и показала его актерскую разноплановость, выведя его из амплуа злодея-боевика.

Эвклид Кюрдзидис в фильме «Жизнь после жизни»

На сегодняшний день Кюрдзидис является востребованным актером российского кино. Его неординарная внешность позволяет играть иностранцев, а актерские способности открывают перед ним широкий диапазон ролей: начиная комедийными персонажами, заканчивая серьезными и лирическими образами. Артист часто снимается в сериалах, но выбирает только те ленты, которые могут привлечь его оригинальным сценарием и неординарными персонажами. На сегодняшний день его фильмография насчитывает более пятидесяти различных картин.

Общие сведения

Математики называют алгоритм Евклида для нахождения НОД взаимным вычитанием. Древнегреческий ученый впервые применил его для двух целых чисел. Позднее это новшество использовалось для нахождения наибольшей величины делителя двух однородных величин (отрезков, земельных участков и т. д. ). Он является старым и эффективным численным алгоритмом. Его применение следует объяснять для пары положительных целых чисел, хотя можно использовать правило и для десятичных дробей. Его изучают в старших классах.

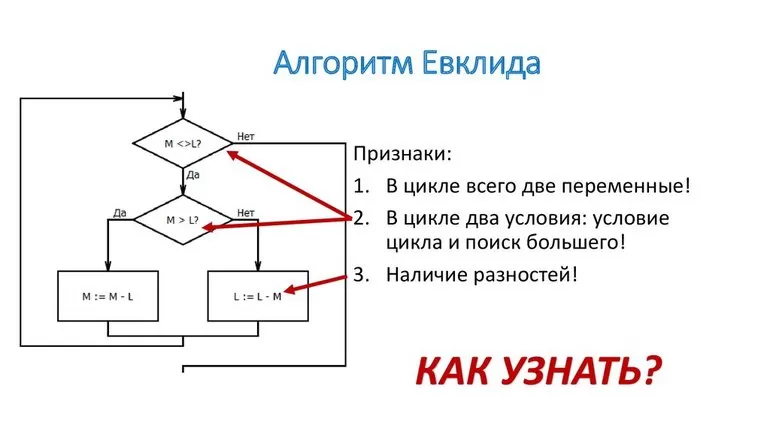
Суть алгоритма заключается в формировании новой пары чисел из меньшего и разницы между большим и меньшим элементом. Процесс, состоящий из арифметических операций, повторяется до тех пор, пока числа не будут равны друг другу. Первоначально инструкция создавалась для натуральных чисел и геометрических величин. Однако в XIX веке ее расширили и стали применять для других объектов: целых чисел Гаусса и многочленов с одной переменной (полиномов). Направление, получившееся в математике, специалисты стали называть евклидовым кольцом. Позднее его доработали и стали применять для узлов и многомерных полиномов.